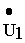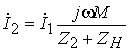Трансформатор без сердечника своими руками

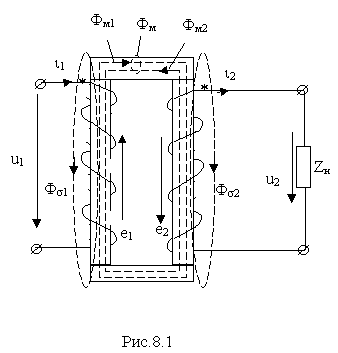
Трансформатор без сердечника своими руками

Трансформатор, вообще, представляет собой аппарат, предназначенный для преобразования посредством магнитного поля электрической энергии переменного тока одного напряжения в электрическую энергию переменного тока другого напряжения при условии сохранения неизменной частоты. Они строятся на базе индуктивно-связанных катушек, надетых на общий сердечник (рис.8.1). У воздушного трансформатора сердечник неферромагнитный.

Обмотка трансформатора, подключенная к источнику с напряжением u 1 , называется первичной обмоткой, а обмотка, к которой подключается нагрузка Z н , называется вторичной обмоткой. Число витков первичной обмотки обозначим через w 1 , а число витков вторичной обмотки — через w 2 .

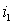
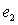
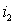
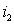
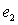
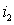
При подключении первичной обмотки к источнику в последней появляется ток , создающий магнитный поток Ф 11 . Часть этого потока Ф м1 , называемая потоком взаимоиндукции первичной обмотки, пронизывает витки вторичной обмотки и обуславливает появление ЭДС в витках вторичной обмотки. Под действием этой ЭДС в цепи нагрузки появляется ток , создающий поток вторичной обмотки Ф 22 . Часть потока, создаваемого током — Ф м2 , пронизывает витки первичной обмотки, замыкаясь встречно потоку Ф м1 первичной обмотки /в соответствии с принципом Ленца/, обуславливающим ЭДС и ток . Таким образом, первичную и вторичную обмотки трансформатора можно рассматривать как две индуктивно-связанные и встречно включенные катушки.

Основные уравнения и векторная диаграмма воздушного трансформатора

Поскольку первичная и вторичная обмотки трансформатора с параметрами соответственно R 1 ,L 1 и R 2 ,L 2 представляют собой 2 индуктивно связанные и встречно включенные катушки, уравнения Кирхгофа, составленные для цепей первичной и вторичной обмоток можно записать в следующем виде

,

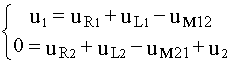
где u R1 , u R1 — напряжения на активных сопротивлениях первичной и вторичной обмоток трансформатора, u L1 , u L2 — напряжения на индуктивностях первичной и вторичной обмоток, u м12 — напряжение взаимоиндукции в первичной обмотке, обусловленное током вторичной обмотки, u м21 — напряжение взаимоиндукции во вторичной обмотке, обусловленное током первичной обмотки, u 2 — напряжение на нагрузке.

Поскольку ток во вторичной обмотке обусловлен напряжением взаимоиндукции u м21 , то это слагаемое во втором уравнении целесообразно перенести в левую часть и записать систему в виде

. (8.1)

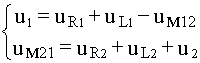
Если напряжение на первичной обмотке трансформатора синусои-дально, то систему (8.1) можно записать в комплексной форме

(8.2)

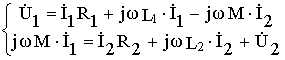
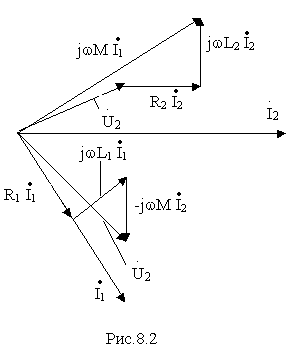
Графической интерпретацией системы (8.2) является векторная диаг-рамма воздушного трансформатора, представленная на рис. 8.2.

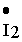
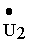
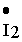
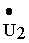
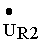
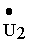
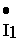
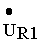
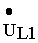
При построении диаграммы считаются заданными векторы тока и напряжения на нагрузке , . Данная диаграмма соответствует активно-индуктивной нагрузке. Диаграмма строится в следующем порядке:

(r) (r) (r) (r) (r) (r) (r) (r) (r) (r)

Входное сопротивление трансформатора.

Вводя понятия комплексного сопротивления первичной обмотки

Z 1 =R 1 +j w L 1 , комплексного сопротивления вторичной обмотки Z 2 =R 2 +j w L 2 и комплексного сопротивления нагрузки Z н , систему (8.2) запишем в виде

(8.3)

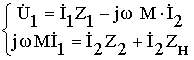
Находя из второго уравнения системы (8.3) ток

и подставляя его в первое уравнение системы, получим

.

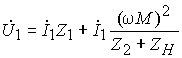
Из последнего выражения найдем входное сопротивление трансформатора в виде

= Z 1 + Z вн .

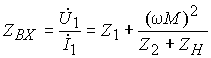
Следовательно, входное сопротивление трансформатора можно представить суммой 2 составляющих : комплексного сопротивления соб-ственно первичной обмотки трансформатора Z 1 и комплексного сопро-тивления Z вн , вносимого из вторичной цепи трансформатора в первичную. Именно изменением этой составляющей можно объяснить изменение тока первичной обмотки трансформатора с изменением его нагрузки.

Уравнения электрического состояния воздушного трансформатора.

В силу того , что поток Ф 11 , создаваемый током первичной обмотки трансформатора имеет 2 составляющие, т.е. Ф 11 = Ф s 1 +Ф м1 , индуктивность первичной обмотки также можно представить в виде суммы двух составляющих L 1 = L s 1 +L м1 первая из которых обусловлена потоком рассеяния первичной обмотки и называется индуктивностью рассеяния первичной обмотки L s 1 , а вторая L м1 обусловлена потоком взаимоиндукции первичной обмотки — Ф м1 и определяется выражением

L м1 = Ф м1 w 1 / i 1 = ( i 1 w 1 l м )w 1 w 2 /( i 1 w 2 )= (w 1 / w 2 )M.

Рассуждая аналогично, индуктивность вторичной обмотки также можно представить в виде суммы двух составляющих L 2 = L s 2 +L м2 , где

L м2 = Ф м2 w 2 / i 2 = ( i 2 w 2 l м )w 2 w 1 /( i 2 w 1 )= (w 2 / w 1 )M.

С учетом сказанного систему уравнений (8.2) можно привести к следующему виду

. (8.4)

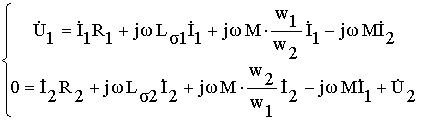
Введем понятие результирующего потока взаимоиндукции /или рабочего потока/ трансформатора. Это результирующий поток, пронизывающий как первичную, так и вторичную обмотки трансформатора. Мгновенное значение этого потока равно

Ф м = Ф м1 — Ф м2 = ( i 1 w 1 l м )- ( i 2 w 2 l м )= i 1 M/w 2 — i 2 M/w 1 ,

Следовательно, ЭДС e 1 и e 2 , наводимые рабочим потоком транс-форматора в витках первичной и вторичной обмоток можно представить в виде

,

,

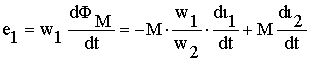
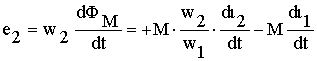
или в комплексной форме

,

.

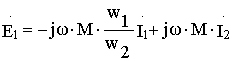
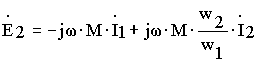
Тогда систему уравнений электрического состояния трансформатора (8.4) можно переписать в виде

, (8.5)

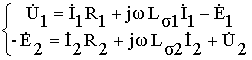
Поскольку рабочий поток трансформатора синусоидален

,

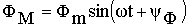
то мгновенные значения ЭДС могут быть определены как

,

.

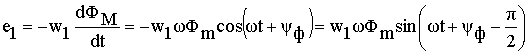
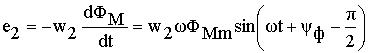
Таким образом, ЭДС e 1 и e 2 имеют одинаковую начальную фазу и отстают от рабочего потока на 90 эл. градусов. Действующие значения ЭДС соответственно равны

,

,

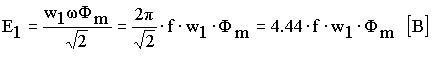
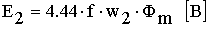
где 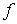— частота питающей сети Ф m — амплитуда рабочего потока трансформатора.

Отношение ЭДС, наводимых рабочим потоком в витках первичной и вторичной обмоток трансформатора, называется коэффициентом трансфор-мации

.

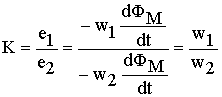
Схема замещения трансформатора и приведение его параметров

При расчете цепей с трансформатором широко используются схемы замещения, при переходе к которым действительные трансформаторные связи /электромагнитные/ заменяются электрическими связями. Эти схемы удобны для аналитического исследования установившегося и переходных режимов в трансформаторе. Схемы составляются таким образом, чтобы их токи и напряжения описывались теми же уравнениями, что и в реальном трансформаторе.

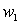
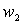
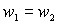
Для обоснования схемы рассмотрим трансформатор с числом витков первичной обмотки равным числу витков вторичной обмотки , то есть . Для такого трансформатора система (8.4) может быть записана в виде

Нетрудно видеть, что в этом случае 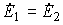. Такая система представляет собой систему уравнений Кирхгофа для электрической цепи, приведенной на рис.8.3, которую можно считать схемой замещения трансформатора для случая, если w 1 =w 2 .

Если число витков первичной и вторичной обмоток различно, то осуществляют приведение параметров трансформатора.

Приведением параметров трансформатора называется операция условной замены действительной вторичной обмотки с числом витков 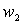фиктивной вторичной обмоткой с числом витков

таким образом, чтобы физические процессы в приведенном трансформаторе оставались такими же, как и в реальном.

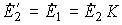
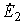
В силу того, что w 2 ‘=w 1 , то , где — ЭДС вторичной обмотки реального трансформатора.

Намагничивающие силы вторичной обмотки реального и приведенного трансформатора должны быть одинаковы, то есть i 2 w 2 = i ‘ 2 w’ 2 .

Следовательно, i ‘ 2 = i 2 w 2 /w’ 2 == i 2 /k, где i ‘ 2 — приведенный ток вторичной обмотки трансформатора.

Полные электромагнитные мощности в нагрузке реального и приве-денного трансформатора должны быть одинаковы, то есть U 2 I 2 = U 2 ‘I 2 ‘ Следовательно, U 2 ‘= U 2 I 2 /I 2 ‘= U 2 k, где U 2 ‘ — приведенное напряжение на нагрузке.

На основе равенства электрических потерь мощности во вторичных обмотках реального и приведенного трансформатора I 2 2 R 2 = I 2 ‘ 2 R 2 ‘, находим

R 2 ‘=(I 2 2 /I 2 ‘ 2 )R 2 =k 2 R 2 , где R 2 ‘ — приведенное активное сопротивление вторичной обмотки.

На основе равенства реактивных мощностей в инуктивностях рассеяния реального и приведенного трансформатора I 2 2 X 2 s = I 2 ‘ 2 X 2 s ‘ нахо-дим X 2 s ‘ =(I 2 2 /I 2 ‘ 2 ) X 2 s = k 2 X 2 s или w L 2 s ‘ =(I 2 2 /I 2 ‘ 2 ) w L 2 s = k 2 w L 2 s , где L 2 s ‘ — приведенная индуктивность рассеяния вторичной обмотки трансформатора.

Приведение параметров нагрузки осуществляется аналогично, т.е.

R н ‘ = R н k 2 , L н ‘ = L н k 2 , C н ‘ = C н /k2.

На схеме (рис.8.3) в скобках приведены условные обозначения элементов приведенного трансформатора.

Под идеальным или идеализированным трансформатором понимают трансформатор, у которого отсутствуют потери энергии на нагрев обмоток и потоки рассеяния обмоток. Поскольку для такого трансформатора R 1 =R 2 =0 и L s 1 = L s 2 =0, то схема замещения его имеет вид, представленный на рис. 8.4. Входное сопротивление трансформатора определяется по формуле

.

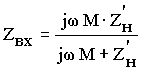
При w M>> Zн Z вх =Z’ н =к 2 Z н .

Следовательно, идеальный трансформатор, включенный между нагрузкой и источником электроэнергии изменяет сопротивление нагрузки пропорционально квадрату коэффициента трансформации без изменения угла. Это свойство практически используется в различных областях техники /электротехники, проводной связи, радио и т.п./ для согласования сопротивлений нагрузки и источника.

Источник