Случайные числа своими руками

Случайные числа не случайны

FullStack CTO

More posts by FullStack CTO.

FullStack CTO

Как создать генератор случайных чисел на JS и предсказать Math.random()

Вы когда-нибудь задумывались, как работает Math.random()? Что такое случайное число и как оно получается? А представьте вопрос на собеседовании — напишите свой генератор случайных чисел в пару строк кода. И так, что же это такое, случайность и возможно ли ее предсказать.

Генератор псевдослучайных чисел и генератор случайных чисел

Для того, чтобы получить что-то случайное, нам нужен источник энтропии, источник некого хаоса из который мы будем использовать для генерации случайности.

Этот источник используется для накопления энтропии с последующим получением из неё начального значения (initial value, seed), которое необходимо генераторам случайных чисел (ГСЧ) для формирования случайных чисел.

Генератор ПсевдоСлучайных Чисел использует единственное начальное значение, откуда и следует его псевдослучайность, в то время как Генератор Случайных Чисел всегда формирует случайное число, имея в начале высококачественную случайную величину, которая берется из различных источников энтропии.

Энтропия — это мера беспорядка. Информационная энтропия — мера неопределённости или непредсказуемости информации.

Выходит, что чтобы создать псевдослучайную последовательность нам нужен алгоритм, который будет генерить некоторую последовательность на основании определенной формулы. Но такую последовательность можно будет предсказать. Тем не менее, давайте пофантазируем, как бы могли написать свой генератор случайных чисел, если бы у нас не было Math.random()

ГПСЧ имеет некоторый алгоритм, который можно воспроизвести.
ГСЧ — это получение чисел полностью из какого либо шума, возможность просчитать который стремится к нулю. При этом в ГСЧ есть определенные алгоритмы для выравнивания распределения.

Придумываем алгоритм ГПСЧ

Генератор псевдослучайных чисел (ГПСЧ, англ. pseudorandom number generator, PRNG) — алгоритм, порождающий последовательность чисел, элементы которой почти независимы друг от друга и подчиняются заданному распределению (обычно равномерному).

Мы можем взять последовательность каких-то чисел и брать от них модуль числа. Самый простой пример, который приходит в голову. Нам нужно подумать, какую последовательность взять и модуль от чего. Если просто в лоб от 0 до N и модуль 2, то получится генератор 1 и 0:

Эта функция генерит нам последовательность 01010101010101… и назвать ее даже псевдослучайной никак нельзя. Чтобы генератор был случайным, он должен проходить тест на следующий бит. Но у нас не стоит такой задачи. Тем не менее даже без всяких тестов мы можем предсказать следующую последовательность, значит такой алгоритм в лоб не подходит, но мы в нужном направлении.

А что если взять какую-то известную, но нелинейную последовательность, например число PI. А в качестве значения для модуля будем брать не 2, а что-то другое. Можно даже подумать на тему меняющегося значения модуля. Последовательность цифр в числе Pi считается случайной. Генератор может работать, используя числа Пи, начиная с какой-то неизвестной точки. Пример такого алгоритма, с последовательностью на базе PI и с изменяемым модулем:

Но в JS число PI можно вывести только до 48 знака и не более. Поэтому предсказать такую последовательность все так же легко и каждый запуск такого генератора будет выдавать всегда одни и те же числа. Но наш генератор уже стал показывать числа от 0 до 9. Кстати, так выглядит распределение по выпадению чисел при 10000 итерациях:

Распределение очень неравномерное, но мы получим генератор чисел от 0 до 9.

Мы можем взять не число Pi, а время в числовом представлении и это число рассматривать как последовательность цифр, причем для того, чтобы каждый раз последовательность не повторялась, мы будем считывать ее с конца. Итого наш алгоритм нашего ГПСЧ будет выглядеть так:

Вот это уже похоже на генератор псевдослучайных чисел. И тот же Math.random() — это ГПСЧ, про него мы поговорим чуть позже. При этом у нас каждый раз первое число получается разным.

Собственно на этих простых примерах можно понять как работают более сложные генераторы случайных числе. И есть даже готовые алгоритмы. Для примера разберем один из них — это Линейный конгруэнтный ГПСЧ(LCPRNG).

Линейный конгруэнтный ГПСЧ

Линейный конгруэнтный ГПСЧ(LCPRNG) — это распространённый метод для генерации псевдослучайных чисел. Он не обладает криптографической стойкостью. Этот метод заключается в вычислении членов линейной рекуррентной последовательности по модулю некоторого натурального числа m, задаваемой следующей формулой:

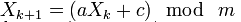
где a(multiplier), c(addend), m(mask) — некоторые целочисленные коэффициенты. Получаемая последовательность зависит от выбора стартового числа — т.е. seed. При разных значениях seed получаются различные последовательности случайных чисел. Пример реализации такого алгоритма на JavaScript:

Многие языки программирования используют LСPRNG (но не именно такой алгоритм(!)).

Как говорилось выше, такую последовательность можно предсказать. Так зачем нам ГПСЧ? Если говорить про безопасность, то ГПСЧ — это проблема. Если говорить про другие задачи, то эти свойства — могут сыграть в плюс. Например для различных спец эффектов и анимаций графики может понадобиться частый вызов random. И вот тут важны распределение значений и перформанс! Секурные алгоритмы не могут похвастать скоростью работы.

Еще одно свойство — воспроизводимость. Некоторые реализации позволяют задать seed, и это очень полезно, если последовательность должна повторяться. Воспроизведение нужно в тестах, например. И еще много других вещей существует, для которых не нужен безопасный ГСЧ.

Как устроен Math.random()

Метод Math.random() возвращает псевдослучайное число с плавающей запятой из диапазона [0, 1) , то есть, от 0 (включительно) до 1 (но не включая 1), которое затем можно отмасштабировать до нужного диапазона. Реализация сама выбирает начальное зерно для алгоритма генерации случайных чисел; оно не может быть выбрано или сброшено пользователем.

Как устроен алгоритм Math.random() — интересный вопрос. До недавнего времени, а именно до 49 Chrome использовался алгоритм MWC1616:

Именно этот алгоритм генерит нам последовательность псевдослучайных чисел в промежутке между 0 и 1.

UPD

Исправил ошибку в алгоритме MWC1616 (пропущенные скобки). Эта же ошибка повторяется и в статье https://v8project.blogspot.ru/2015/12/theres-mathrandom-and-then-theres.html

то видим, что должны быть скобки:

Предсказываем Math.random()

Чем это было чревато? Есть такой квест: https://alf.nu/ReturnTrue

В нем есть задача:

Что нужно вписать вместо вопросов, чтобы функция вернула true? Кажется что это невозможно. Но, это возможно, если вы заглядывали в спеку и видели алгоритм ГПСЧ V8. Решение этой задачи в свое время мне показал Роман Дворнов:

Этот код работал в 70% случаев для Chrome

Видите эти равномерности на левом слайде? Изображение показывает проблему с распределением значений. На картинке слева видно, что значения местами сильно группируются, а местами выпадают большие фрагменты. Как следствие — числа можно предсказать.

Выходит что мы можем отреверсить Math.random() и предсказать, какое было загадано число на основе того, что получили в данный момент времени. Для этого получаем два значения через Math.random(). Затем вычисляем внутреннее состояние по этим значениям. Имея внутреннее состояние можем предсказывать следующие значения Math.random() при этом не меняя внутреннее состояние. Меняем код так так, чтобы вместо следующего возвращалось предыдущее значение. Собственно все это и описано в коде-решении для задачи random4. Но потом алгоритм изменили (подробности читайте в спеке). Его можно будет сломать, как только у нас в JS появится нормальная работа с 64 битными числами. Но это уже будет другая история.

Новый алгоритм выглядит так:

Его все так же можно будет просчитать и предсказать. Но пока у нас нет “длинной математики” в JS. Можно попробовать через TypedArray сделать или использовать специальные библиотеки. Возможно кто-то однажды снова напишет предсказатель. Возможно это будешь ты, читатель. Кто знает ?

Сrypto Random Values

Метод Math.random() не предоставляет криптографически стойкие случайные числа. Не используйте его ни для чего, связанного с безопасностью. Вместо него используйте Web Crypto API (API криптографии в вебе) и более точный метод window.crypto.getRandomValues() .

Пример генерации случайного числа:

Но, в отличие от ГПСЧ Math.random(), этот метод очень ресурсоемкий. Дело в том, что данный генератор использует системные вызовы в ОС, чтобы получить доступ к источникам энтропии (мак адрес, цпу, температуре, etc…).

Материалы про Math.random()

Больше про random в спецификации:

Хорошая статья про работу рандомайзера

Пример реализации предсказателя с Math.random()

Кстати, следить за обновлениями и прочими материалами от меня можно в телеграм канале: @prowebit

В этом канале публикую не только статьи из этого блога, но и различные новости и мысли. Подписывайтесь ?

Источник

Случайные числа

Я думаю понятие случайных чисел/величин вам знакомо: они случайны. Иногда в самодельном устройстве бывает нужна случайная величина, например для какой-нибудь игры или световых эффектов. Программный источник настоящих случайных чисел организовать весьма непросто, в отличие от аппаратного. Банально игральный кубик или лото-машина являются вполне себе хорошими источниками случайных чисел. Микроконтроллер к слову не может генерировать случайные числа, потому что он – точное вычислительное устройство, случайностей быть не может. Что делать? Использовать такое понятие, как псевдослучайные числа. Чем они отличаются от случайных? Своей природой. Псевдослучайное число получается путём различных математических действий с начальным числом, то есть имея начальное число, мы можем сгенерировать на его основе целую кучу других чисел. Но тут есть две проблемы:

• Через какое-то количество чисел (тысяч, а может и миллиардов, а может и больше) ряд сгенерированных псевдослучайных чисел начнёт повторяться. Для наших целей это не так страшно, можно об этом не думать
• Генератору псевдослучайных чисел нужно начальное случайное число. Вот это реально беда… Но ничего, у нашего микроконтроллера есть и аппаратные средства

Ардуино и случайные числа

Ардуино имеет пару готовых функций для работы с псевдослучайными числами, давайте на них посмотрим:

• random(max); – возвращает псевдослучайное число в диапазоне от 0 до ( max – 1 ). max принимает unsigned long , то есть от 0 до 4 294 967 295
• random(min, max); – возвращает псевдослучайное число в диапазоне от min до ( max – 1 ). max принимает unsigned long , то есть от 0 до 4 294 967 295
• randomSeed(value); – дать генератору псевдослучайных чисел новую опорную точку для отсчёта. value – любое число типа unsigned long , значит на Ардуино мы имеем 2^32 (4 294 967 295) наборов псевдослучайных чисел. На ваш век этого точно хватит!

Как правильно генерировать случайные числа, чтобы последовательность каждый раз была новая? Есть варианты:

• При запуске программы задавать случайное число в randomSeed() . Как это сделать? Расскажу ниже
• Если устройство как-то взаимодействует со внешним миром, или даже с пользователем, то можно при наступлении некоторых аппаратно случайных событий (нажатие кнопки, срабатывание датчика, принятие данных, и т.д.) скармливать randomSeed‘у текущее время с момента старта программы, т.е. функции millis() или micros() . Отличное решение кстати! Банально вызываем randomSeed(micros()) и всё.

Аппаратный рандом

Помните, в уроке про цифровые пины я говорил, что если пин никуда не подключен – то он ловит “из воздуха” всякие наводки. Шумы имеют природу, близкую к случайной, и было бы глупо этим не воспользоваться! Давайте посмотрим, какие значения можно получить с никуда не подключенного аналогового пина, опрашивая его обычным analogRead();

Синусоида? Вполне логично, в стенах куча проводов с сетевым напряжением, вот они и наводят на микроконтроллер всякие помехи. Можно ли пользоваться сырым значением с аналогового пина в качестве “зерна” для randomSeed() ? Нужно! То есть при запуске устройства делать вот так:

Но есть ещё интересный вариант, который позволит получить гораздо более случайные числа для randomSeed() . Есть информация, что первые два бита из результата analogRead() имеют самый большой шум. Давайте на него посмотрим, выведя несколько (300) результатов в график. Получить первые два бита можно так: analogRead(A0) & 0b0000011 , или более коротко – analogRead(A0) & 3

Выглядит весьма случайно, никакой закономерности не прослеживается! Но значения меняются всего от 0 до 3. Поэтому можно попробовать их перемножать и складывать, примерно так:

Именно такой код я рекомендую использовать для получения случайного зерна для генератора случайных чисел при запуске программы. Напоследок давайте посмотрим, какой результат даёт такая конструкция:

График я построил в excel, чтобы более чётко видеть рассеивание полученного случайного значения Имеем практически равномерное рассеяние и огромное количество случайных значений, полученных путём перемножения и сложения “шума”. Пользуйтесь на здоровье.

Случайный bool

Иногда бывает нужен случайный флаг, то есть true / false . Делается это очень просто: в уроке про условия я рассказывал, что bool ( boolean ) принимает true при любом отличном от нуля значении. Это можно использовать для получения случайного true / false с заданной вероятностью! Просто присваиваем логической переменной результат функции random() , в которую передаём число, обратное вероятности получения false :

Переменная rndFlag получит значение false с вероятностью 1/5, то есть 20%. Если нужен true с низкой вероятностью – используем инверсию:

Теперь переменная rndFlag получит значение true с вероятностью 10%.

Видео

Источник